Данная норма говорит нам о том, что любые из двух (именно движущих) волн в импульсе с большой вероятностью окажутся равными как по времени, так и по величине. Данная норма особенно верна в том случае, если одна из движущих волн растянута, и верна вдвойне, если растянута именно третья волна в импульсе. Но даже если две волны не являются равными по времени и по величине, они с большой вероятностью будут связанны друг с другом коэффициентом 0,618. Также команда Пректера нашла закономерность, которая говорит нам о том, что, если волны крупнее волн промежуточной степени, их величину и продолжительность лучше измерять в процентах.
Практические примеры равенства волн
Посмотрим на график Промышленного индекса Доу-Джонса. С 1942 года по 1966 год развивалась волна III. В этой III волне волна [3] of III растянута, а значит волны [1] и [5] по норме равенства волн должны быть одинаковы или связанны друг с другом коэффициентом 0,618. Команда Пректера посчитала, что волна [1] of III выросла на 120 п., а это 129% роста за 49 месяцев. А вот волна [5] of III выросла на 438 п., а это 80% роста за 40 месяцев (рост в 129% умножаем на коэффициент 0,618). Эти данные колоссально отличаются от роста третьей волны, которая длилась 126 месяцев и увеличилась в 324%. Также мы можем открыть платформу Tradingview, взять инструмент «коррекция по Фибоначчи», измерить им длину волны [1] of III, перенести полученные данные на начало волны [5] of III, и увидим, что волна [5] of III закончилась в районе коэффициентов 0.618-0,786 (см. рис. 5-5).
(Рис.5.5)
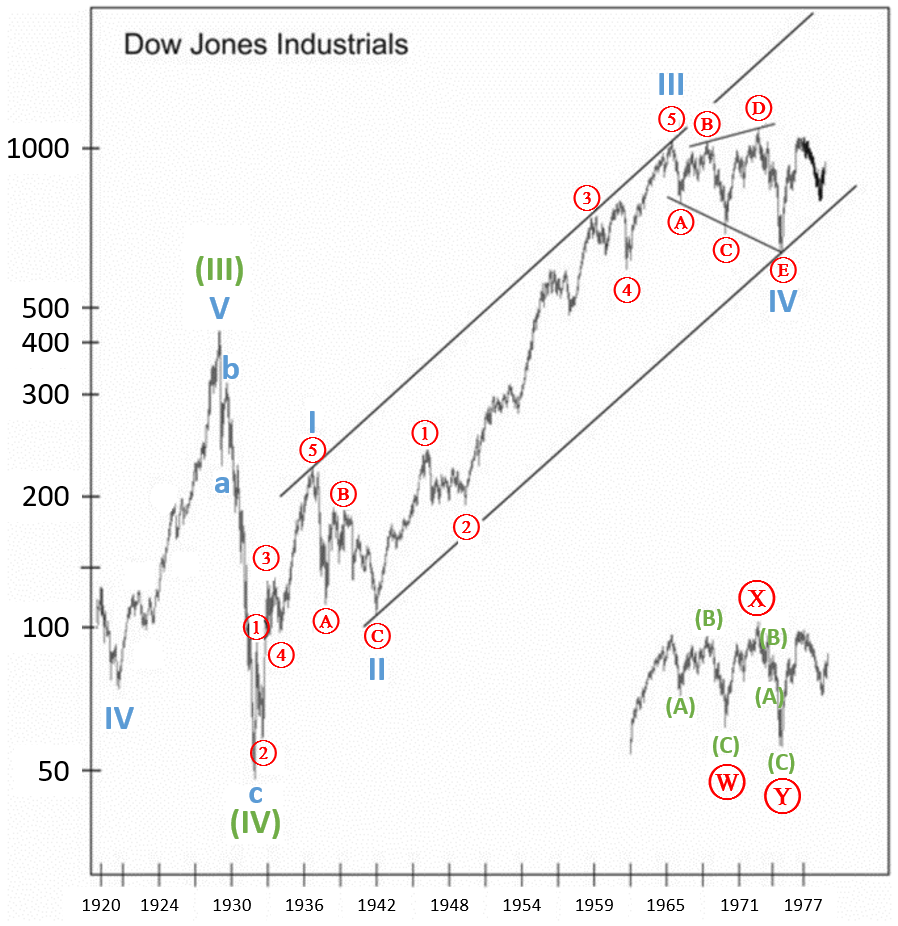
Если мы хотим измерить равенство в волнах промежуточных степеней (или даже рассмотреть более мелкие степени), мы можем устанавливать его арифметическим методам, не прибегая к процентам, и не усложняя подсчеты. Так как команда Пректера заявляет, что процентные величины будут совпадать с абсолютными с огромной вероятностью. Обратим внимание на конец 1976 года на график Промышленного индекса Доу-Джонса. Волна 1 младшей степени выросла на 35,24 п. за 47 часов, и волна 5 длилась 47 часов и выросла на 34,4 п. (волна 3 была растянута). Данный пример показывает нам, что норма растяжения волн часто является крайне точной.


